(二)计算机的计算方法[计组]

转载自：计算机组成原理 – Here_SDUT (fangkaipeng.com)

根据实际学习内容有一定的添加以及修改

2.1 数据与文字的表示方式

2.1.1 实际数的表示方法

1.定点数表示法

将数据分为纯整数和纯小数两类，用n+1位表示一个定点数，x_n为符号位，放在最左边，0表示正号，1表示负号。

故一个数 x 可以表示为 x=x_nx_n−1…x₁x₀

定点小数 x为纯小数：0≤|x|≤1−2−n

定点整数 x为纯整数：0≤|x|≤2n−1

计算机中多采用定点纯整数表示，将定点数表示的运算简称整数运算。

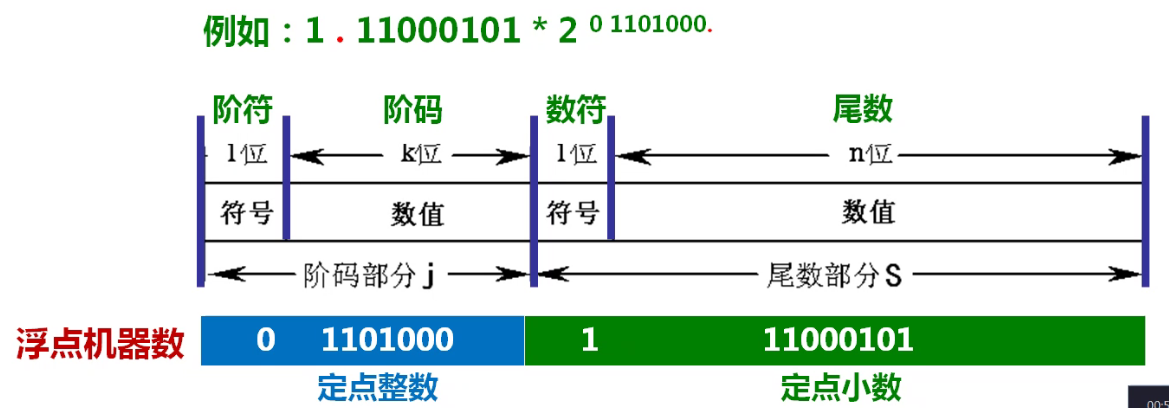
2.浮点数表示法

任何一个数都可以写成浮点数形式

小数点随着阶码的不同而浮动，数的范围和精度分别表示。

格式：N=S*r^j

• r : 基数, r=2 (与当前的数字的进制有关)
• j : 阶码, 带符号的纯整数(定点整数)
• S: 尾数, 带符号的纯小数(定点小数)

在机器中，尾数用定点小数形式表示，指数用定点整数形式表示，称为阶码。

3. 浮点数表示范围

4. 浮点数的规格化

规格化形式：

• 基数 r = 2 ，尾数最高位为 1
• 基数 r = 4 ，尾数最高 2 位不全为 0
• 基数 r = 8 ，尾数最高 3 位不全为 0

基数不同，浮点数的规格化形式不同。

规格化方式：

• r = 2 左规 尾数左移 1 位，阶码减 1
  右规 尾数右移 1 位，阶码加 1
• r = 4 左规 尾数左移 2 位，阶码减 1
  右规 尾数右移 2 位，阶码加 1
• r = 8 左规 尾数左移 3 位，阶码减 1
  右规 尾数右移 3 位，阶码加 1

基数 r 越大，可表示的浮点数的范围越大，基数 r 越大，浮点数的精度降低。
举例：

1.设 m = 4，n = 10，r = 2，求尾数规格化后的浮点数表示范围。

最大正数 = 2+1111∗0.1111111111=215∗(1−2−10)

最小正数 = 2−1111∗0.1000000000=2−15∗(2−1)=2−16 （尾数第一位规格化后必须为1）

最大负数 = 2−1111∗−0.1000000000=−2−15∗2−1=−2−16

最小负数 – 2+1111∗−0.1111111111=−215∗(1−2−10)

例 6.13 将 x = + 19/128 写成二进制定点数、浮点数及在定点机和浮点机中的机器数形式。其中数值部分均取 10 位，数符取 1 位，浮点数阶码取 5 位（含1位阶符），尾数规格化。

x的二进制表示: 设 x = + 19/128

二进制形式： x=0.0010011

定点表示： x=0.0010011000

浮点规格化： x=0.1001100000∗2−10

定点机中： 原补反 [x]_原=[x]_补=[x]_反=0.0010011000

浮点机中：
原；[x]_原=1,0010；0.1001100000
补；[x]_补=1,1110；0.1001100000
反；[x]_反=1,1101；0.1001100000

5. 十进制数表示

1. 字符串形式
   即一个字节存放一个十进制的数位或符号位，还需要存放该数在主存中的起始地址和该数的位数。
2. 压缩的十进制数串形式
   即一个字节存放两个十进制的数位或符号位即BCD码(压缩)，即一个字节存放两个十进制的数位或符号位即BCD码(压缩)。

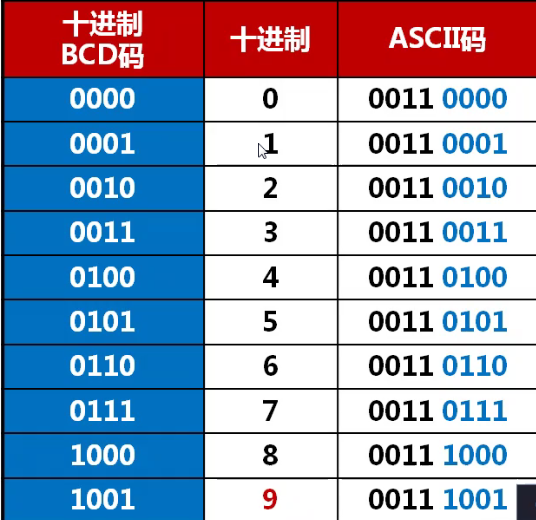
大于9 就需要矫正

• 加6矫正

2.1.2 机器数的表示方法

0.位置表示法的定义

反码与补码加法的理解 | mznote (sbwcwso.com)

• 一个 n位的整数 N会按下面的形式书写`：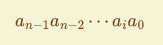

  

  • 其中 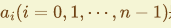是与基数 的幂相乘的系数，即有下式成立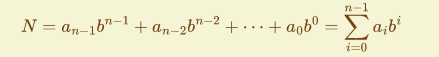

    

  • 对于负数，则会在其前面加上负号 - ，即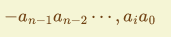

  • 对于二进制，则 b=2

    • 例：十进制数 7 ，-7 表示为 位二制数分别为： 0111, -0111，

人们一般习惯在位置码上进行运算，但计算机不习惯，而且计算机底层不可能用负号来表示负数，

更不可能让负号参与运算，因此引入了原码，反码和补码的概念

1. 原码表示法

原码的定义主要是为了引入符号位

(1) 数学定义

• 整数：

  

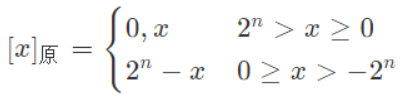
整数的第一位为符号位，用 “,”隔开，0表示正数，1表示负数,x为真值，n为整数的位数。

public void printBinary(int num){
    while(num!=0){
        System.out.print(num&1);
        num>>=1;
    }
}

需要注意的是, 位置表示法中的负号也会参与运算

• 小数：

  

  程序员面试金典4~5 | dhx_'blog (adorabled4.github.io)

  求小数的二进制表示

class Solution {
    public String printBin(double num) {
        StringBuilder sb=new StringBuilder("");
        int cnt=0;// 统计位数, 如果超过32说明小数无法转换, print "error"
        while(num%1!=0){
            if(cnt>=32) return "ERROR";
            num*=2;
            sb.append((int)num);
            if(num>=1){
                num-=1;
            }
           cnt++;
        }
        return "0."+sb.toString();
    }
}

(2) 举例

[x]_原=1.001 => x=−0.001

[x]_原=0.101 =>x=+0.101

[x]_原=1,110 =>x=−110

[x]_原=0,011 =>x=+011

结论：有逗号表示整数，有小数点表示小数，符号前的数表示符号，0表示正数，1表示负数。

(3) 特点

简单、直观，但是在加法运算时由于符号位的存在，不能简单地按位相加，“+0”和“-0”的原码不同。

2.补码表示法

(1) 补的概念

• 以时钟为例，在时钟上进行运算相当于是模12下的运算。如果要-3，有两种途径：把指针向后拨3位（-3）或者向前拨9位（+9），故可以用这种方式将减法转换成加法，我们称+9是-3在模12下的补数。
• 结论：
  1. 一个负数加上“模”就是它的补数（如-3+12=9，表示-3在模为12下的补数是9）。
  2. 一个正数和一个负数互为补数时，他们绝对值之和即为模数（相当于结论1的逆运算）。
  3. 正数的补数就是其本身。
  4. “+0”和“-0”的补码相同

(2) 补码的定义

• 整数：

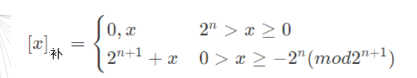
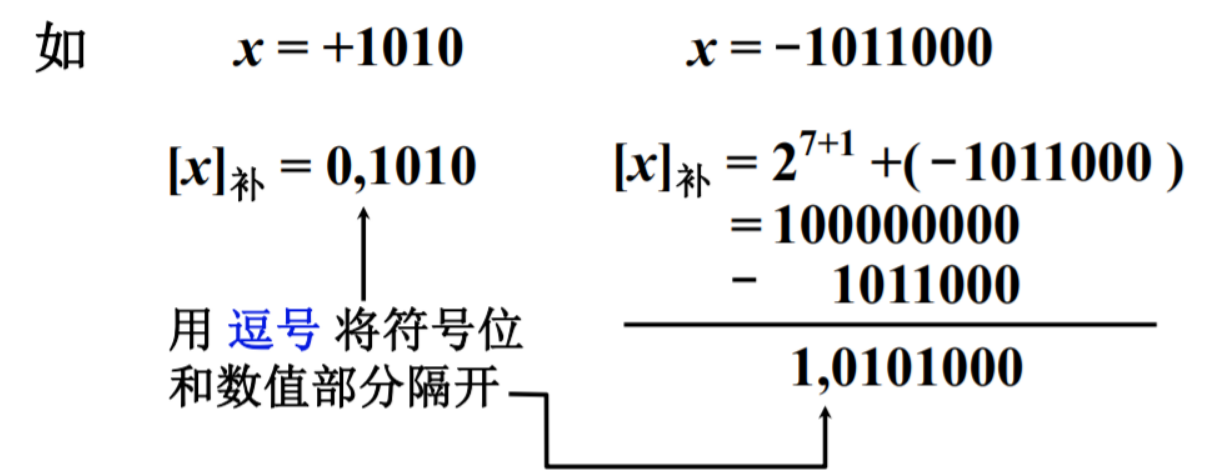
特殊的⭐ :

首先我们要知道 :

当数值的大小超出类型范围的时候, 会发生什么?

例如下面的C代码

printf("val=%d \n", (char)128);

我们将 128 强制转换为了char , 显然这已经超出了char类型的范围(-128~127),

我们知道计算机使用补码来表示数据, 127的二进制表示为01111111 , -128的补码表示为 [x]_补 = 128 = 1000 0000

如果127+1, 那么我们将得到1000 0000, 此时的1000 0000 的真值是-128 。1000 0000是2的补码形式的-128。

因为数值的高位顶飞了正确的符号位

那么我们就得到了 -128, 所以上面的代码的打印结果为val=-128

那么下面的代码我们也就很容易就能理解了

void test2(int n) // 注意补码的计算方法
{
    char c = n;
    char d = -c;
    // 补码计算 c 的补码为 1000 0000    d=-c = 128 的补码为1000 0000 原码为 0000 1000 0000
    /// d实际存储 补码 100 0000  那么 也就是 dc 的补码相同  所以d=c
    printf("10 进制 c=%d, d=%d \n", c, d);
    printf("16 进制 c=%x, d=%x \n", c, d);
}

当我们传入n=-128 ,

根据上面的补码的计算方法, c的补码应该是 : 1000 0000

d=-c = >d=128 超出了char的范围 d又变为了 -128 ,

16进制的结果直接进行进制转换即可

那么上面的代码test2(-128)的打印结果为

10 进制 c=-128, d=-128
16 进制 c=ffffff80, d=ffffff80

• 小数：
  • （勘误：下方公式的下标应该为“补”）

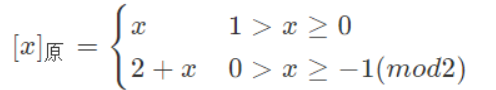
(4) 快速求补码

当真值为负数时，补码可以用原码忽略符号位每位取反后末位+1得到，再将符号位填1。

如：x = -1010,取反得0101,+1得0110,加上符号位得补码：1,0110。

原因如下：

根据补码的最初定义，

[x]_补=2n+1+x，假设x是个4位负数，用 −x₁x₂x₃x₄ 表示，

那么公式可以写成 [x]_补=25–x₁x₂x₃x₄=100000–x₁x₂x₃x₄=11111+00001–x₁x₂x₃x₄ ，

而对于 11111−x₁x₂x₃x₄ 就可以看成 1x1¯x2¯x3¯x4¯ ，然后再加上一个 00001 。即除符号位外，每位取反，末位+1。

所以，已知x的补码，也可以很容易地求得-x的补码，即整体取反+1。

树状数组的关键函数lowbit用于求一个数从末尾开始的第一个1所在位置的十进制数，其实现方式就是x & -x，用的就是这里的原理。

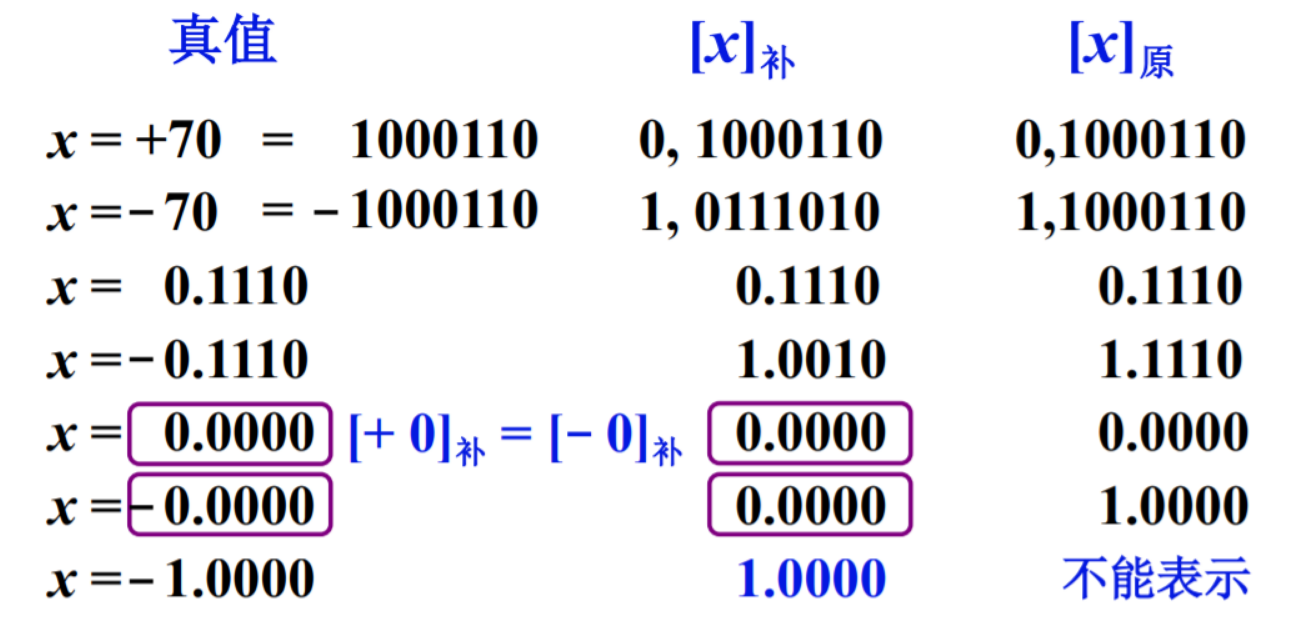
按位取反(符号位不需要取反), 末尾加一 , 从后往前

3.反码表示法

(1) 定义

（勘误：下方公式的下标应该为“反”）

• 整数：

  

• 小数：

即 当真值为负数时，反码可以用原码除符号位外每位取反得到，正数反码不变，“+0”和“-0”的反码不同。

4. 三种表示法小结

• 最高位为符号位，书写上用“,”（整数） 或“.”（小数）将数值部分和符号位隔开。
• 对于正数，原码 = 补码 = 反码。
• 对于负数 ，原码符号位为 1，数值位不变，原码除符号位外取反后得反码，反码末位+1得补码，补码符号位取反得移码，补码连同符号位取反后+1得相反数的补码。

一字节空间可以表示的范围：

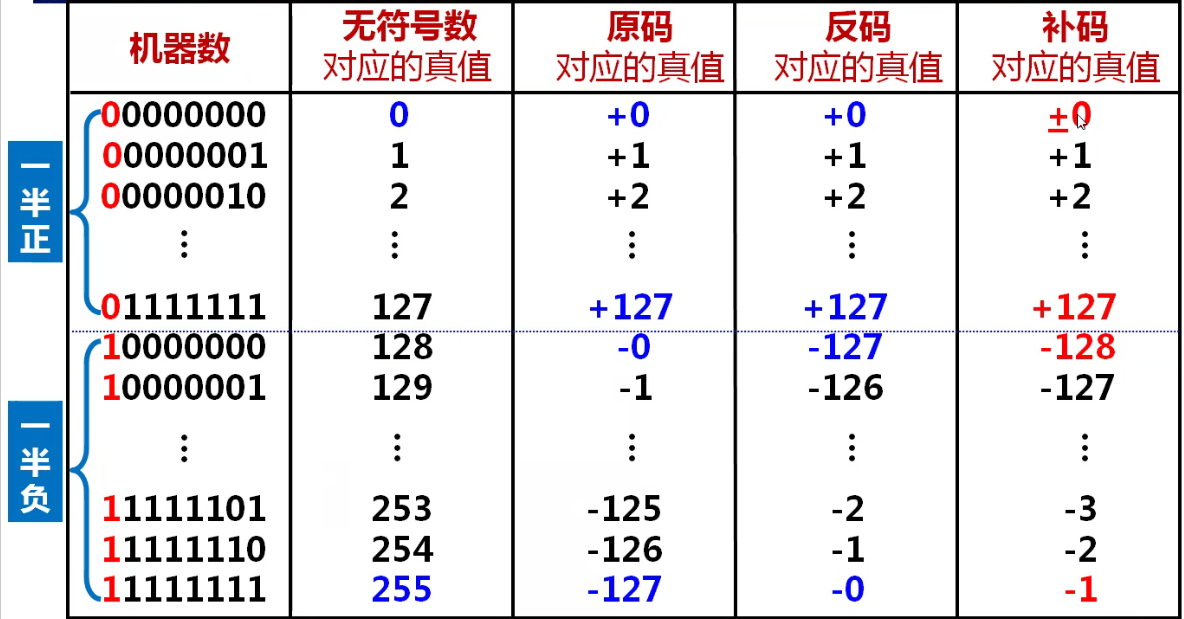
疑问：加蓝处为何为-128？

答：二进制代码10000000表示负数，忽略符号位取反后+1得到其补码也为1000000，如果按照原码的定义，10000000表示-0，但是补码没有“+0”和“-0”之分，补码的0全用00000000表示，多出的“-0”用于表示-128，所以补码比其他都多一个最小数。

5.移码表示法

(1) 定义

由于符号位存在，补码很难直接判断真值大小。

[x]_移=2n+x(2n>x≥−2n)x为真值，n为整数的位数。

x=10100,[x]_移=25+10100=1,10100

x=−10100,[x]_移=25−10100=0,01100

移码与补码只差一个符号位，符号位取反两者就能相互转换。

证明：

正数：[x]_补=0,x [x]_移=2n+x，相当于在第n为 +1，即在符号位取反。

负数：[x]_补=2n+1+x=(2n+x)+2n=[x]_移+2n，也相当于符号位取反。

(2) 特点

移移[+0]移=[−0]移

最小真值的移码为全 0,用移码表示浮点数的阶码,能方便地判断浮点数的阶码大小。

2.1.3字符与字符串的表示方法

符号数据:字符信息用数据表示，如ASCII等;
ASCII:用一个字节来表示,低7位用来编码(128),最高位为校验位，
字符串的存放方法：可以从低位到高位存放也可以从高位到低位存放。

2.1.4 汉字的表示方法

1. 汉字的输入编码

数字编码 拼音码 字形编码

2.汉字内码

汉字信息的存储，交换和检索的机内代码，两个字节组成，每个字节高位都为1(区别于英文字符)。

汉字字模码

用点阵表示汉字字形，形成汉字库。

输入编码用于输入，汉字内码用于计算机内部处理，字模码用于汉字输出。

2.1.5 校验码（奇偶校验）

设x=x0x1…xn−1是一个n位字，奇校验位C定义为：c¯=x0⨁x1⨁…⨁xn−1,即只有x中有奇数个1时才会使得c = 0。
奇偶校验码只能检测奇数个错误，无法检测偶数个错误，更不能提供错误的位置。

2.2定点加减法运算

2.2.1 补码加法

公式：[x]_补+[y]_补=[x+y]_补

补码加法特点： 符号位一起参与运算，在模 2n+1 下运算，即溢出舍去。

2.2.2 补码减法

公式： [x−y]_补=[x]_补–[y]_补=[x]_补+[−y]_补

已知y的补求-y的补方法： 连同符号位取反后末尾+1。

举例

2.2.3 溢出概念与检测方法

1.定义

定点整数机器中，数的表示范围|x|<2n−1 ，在运算过程中出现大于字长绝对值的现象称为溢出。两个正数相加，结果大于机器字长所能表示的最大正数（变成负数），称为正溢。两个负数相加，结果小于所能表示的最小负数，称为负溢。

参加操作的 两个数（减法时即为被减数和“求补” 以后的减数）符号相同，其结果的符号与原操作 数的符号不同，即为溢出

2.双符号位法判断溢出

[x]_补=2n+2+x(mod2n+2)

[x]_补+[y]_补=[x+y]_补(mod2n+2)

规则： 两个符号位一起参与模2n+2下的运算，

符号位为11表示负数，00表示正数，01和10表示溢出，

最高符号位表示正确的符号，01为正溢，10为负溢。

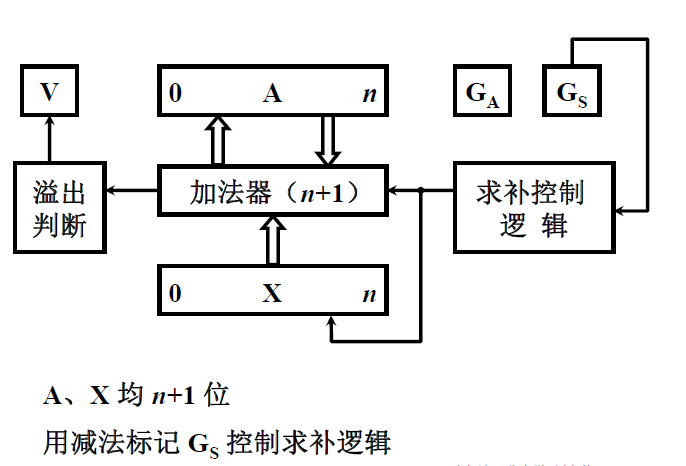
补码加减法的硬件配置

3.单符号判断溢出

当符号位产生进位而最高有效位没进位时发生负溢，当符号位无进位而最高有效位进位时发生正溢。

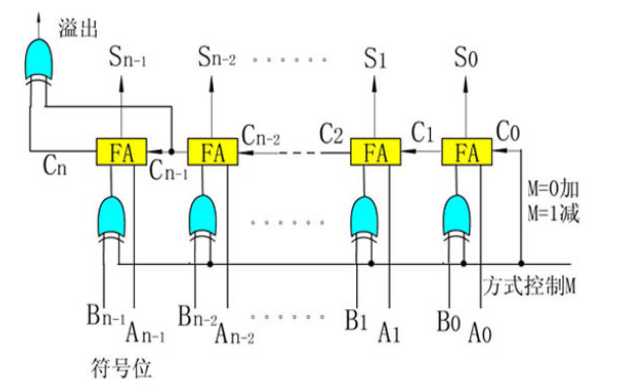
2.2.4 基本的二进制加法/减法器

由n个1位的全加器（FA）串联组成，全加器包含三个输入（两个加数，一个前驱进位数）和两个输出（结果和进位）。M为方式控制输入线，M=0时做加法，M=1时做减法。

减法实现： 通过 补补补[A−B]补=[A]补+[−B]补 实现，-B的补码就是B连同符号位取反后+1，电路中通过一个异或门将B与1异或实现每位取反，C0输入1实现末尾+1。

2.3 定点乘法运算

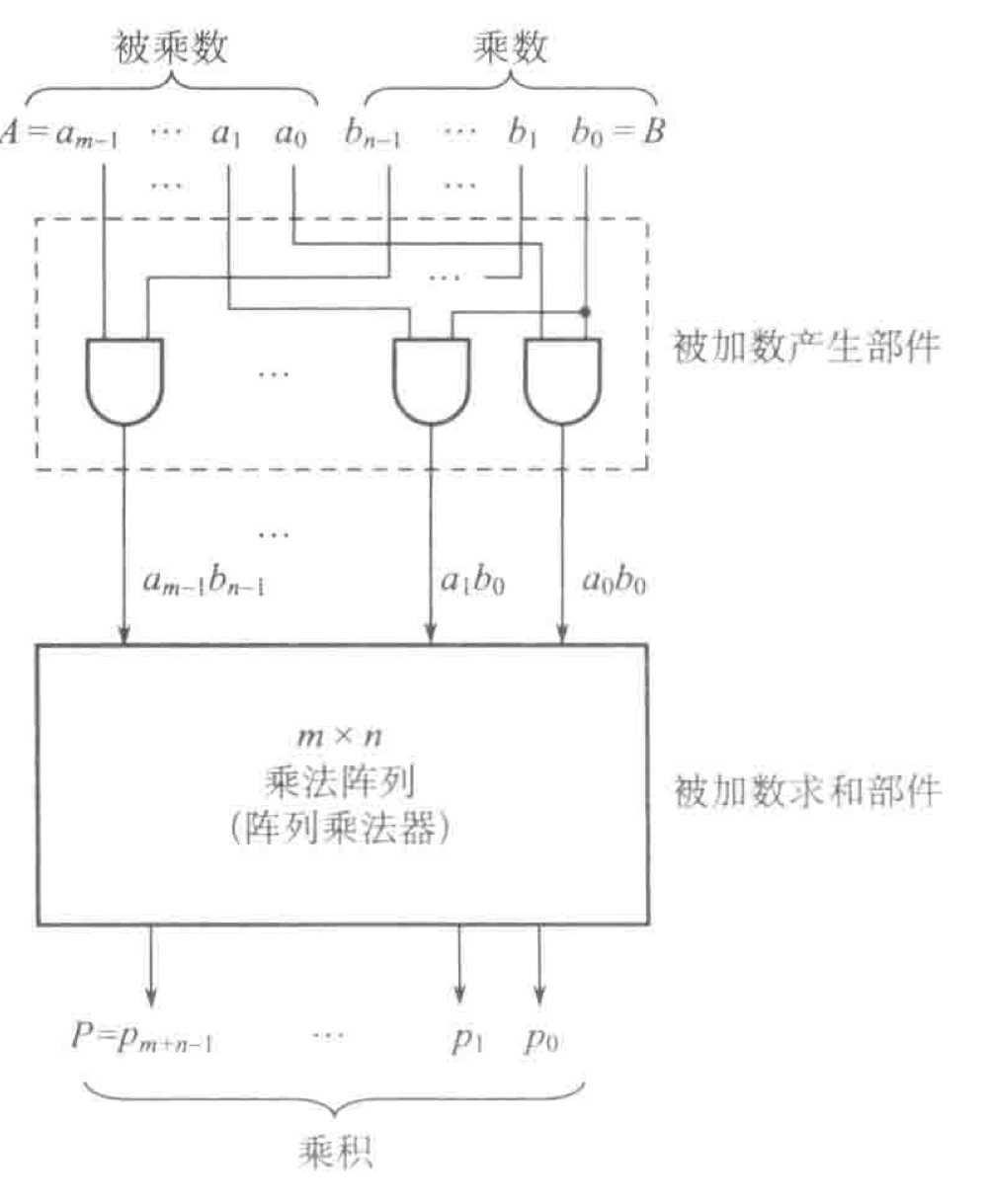
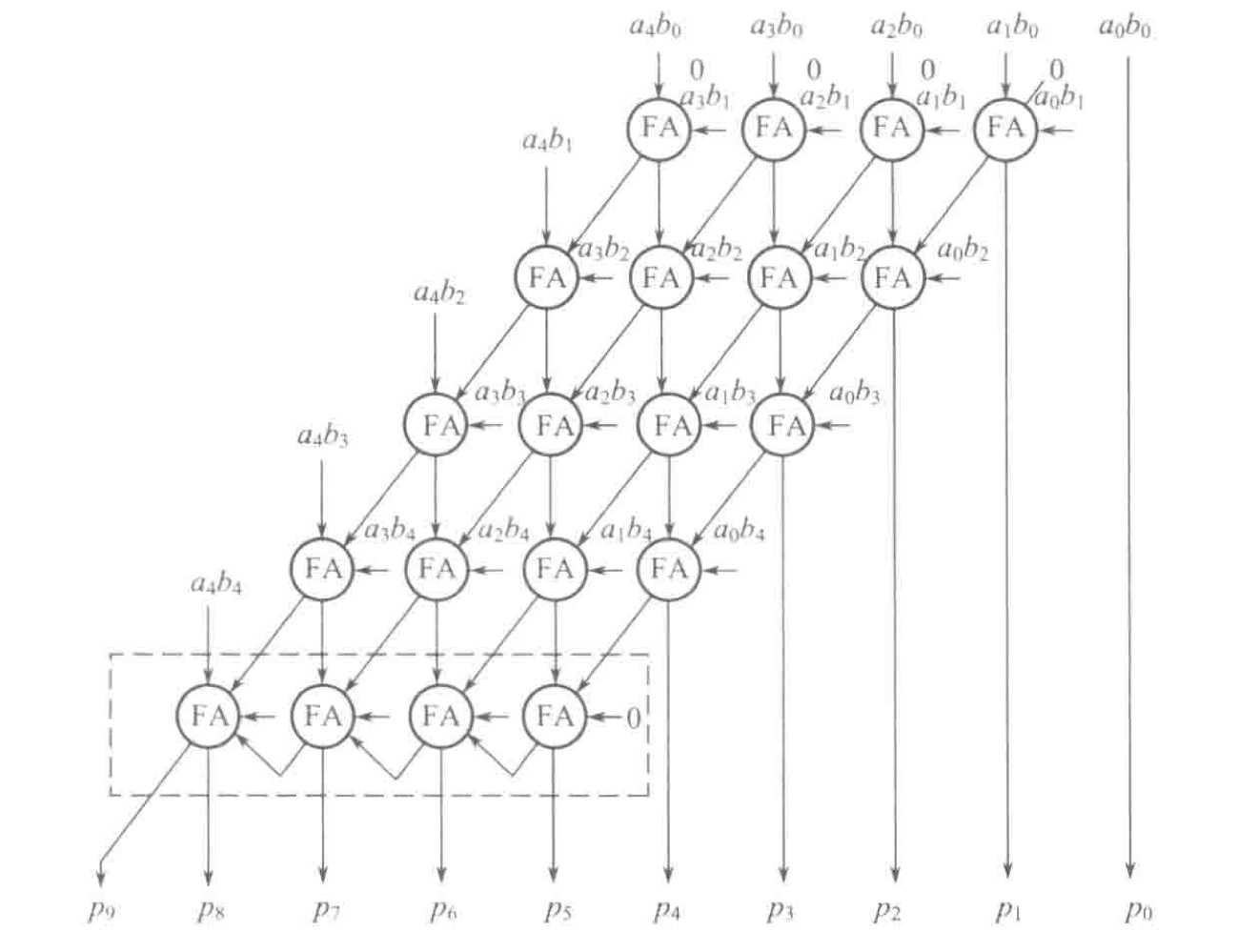
2.3.1 不带符号的列阵乘法器

如图，设A=am−1…a1a0 以及 B=bn−1…b1b0 ,在二进制的乘法中被乘数 A 和乘数 B 产生 m+n 位乘积 P=pm+n−1…p1p0=∑i=0m−1∑j=0n−1(aibj)2i+j，其中每个aibj称为一个被加数。

对于m∗n 个被加数可以用m∗n 个与门并行产生：

产生被加数后需要将其按照上述P的计算公式加起来，可以用一组并行的加法器实现，即列阵乘法器：

2.3.2 带符号的列阵乘法器

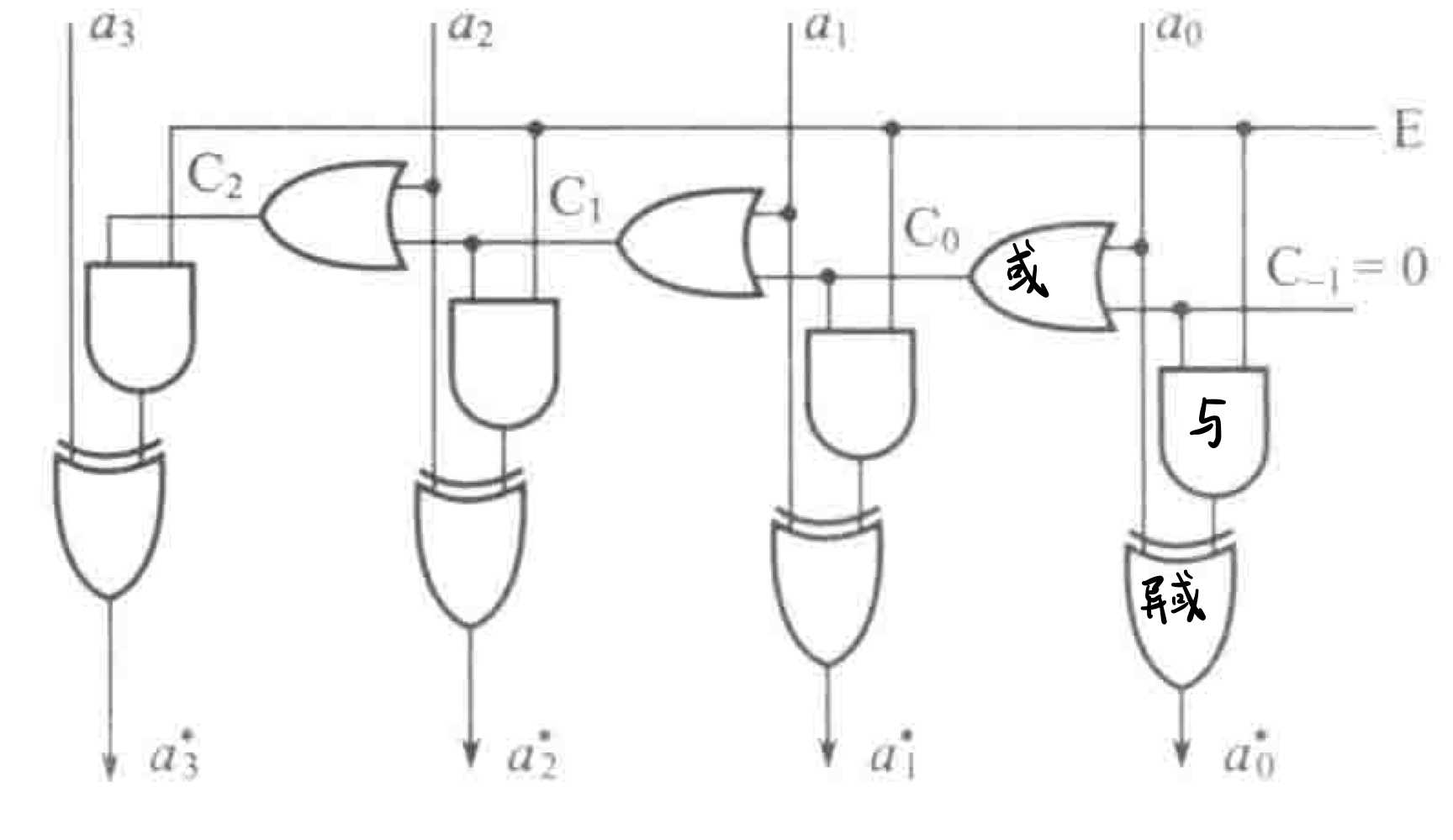
求补方法：从右往左扫描，遇到第一个“1”，将1左边的所有取反，右边连同自己不变，结果就是补码。

求补电路：

如图所示，C−1 始终保持0，E 为控制信号，为1表示进行求补操作。最下方输出的即求补后的结果。

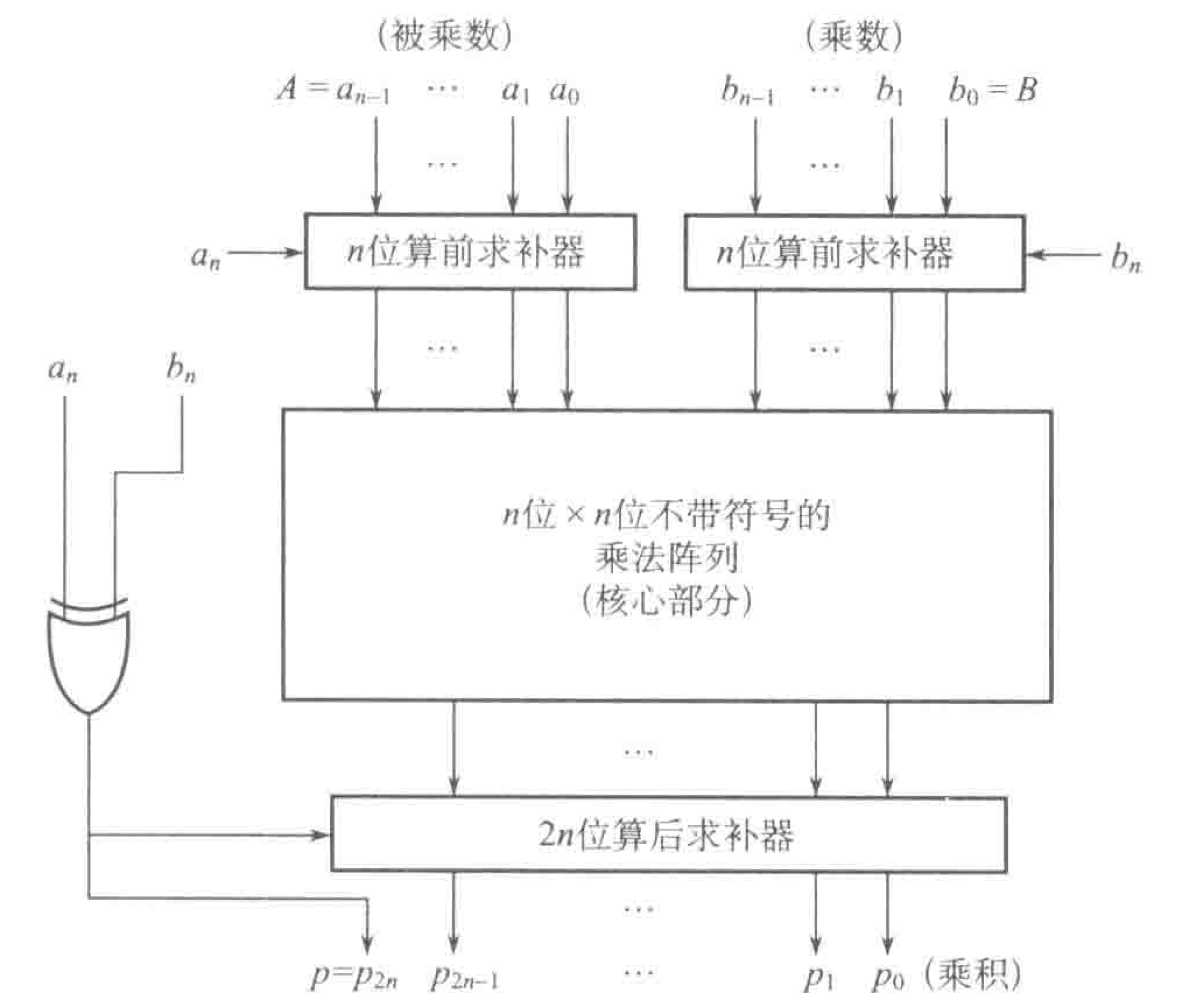
带符号的列阵乘法器含有三个求补器，其中两个为算前求补器，一个位算后求补器，结构如图所示：

使用规则（考）：

• 用于原码列阵乘法器：忽略三个求补器，单独考虑符号位，使用原码输入到乘法列阵运算。

• 用于补码列阵乘法器：单独考虑两个乘数的符号位，将负数的数值部分求补后输入给乘法列阵运算，若符号位异或后为1，则将乘法列阵输出的结果求补后加上符号位，如果符号位为0则直接加上符号位。

例题：

1.设x=+15，y=-13，用带求补器的原码阵列乘法器求出乘积x·y

由于是原码列阵乘法器，首先求出x和y的原码：原，原[x]原=01111，[y]原=11101, 去掉符号位：，|x|=1111，|y|=1101, 符号位运算：0⨁1=1。

            1 1 1 1
×           1 1 0 1
———————————————————
            1 1 1 1
          0 0 0 0
        1 1 1 1
+     1 1 1 1
———————————————————
    1 1 0 0 0 0 1 1
 

乘积符号为1，算后求补器输出11000011，原[x∗y]原=111000011，换算成二进制数真值是：
x∗y=(−11000011)2=(−195)10。

2.设x=-15，y=-13，用带求补器的补码阵列乘法器求出乘积x·y。

补码列阵乘法器，求出补码补，补[x]补=10001，[y]补=10011，乘积符号位运算：1⨁1=0。
忽略符号位后用算前求补器输出 ，|x|=1111，|y|=1101 。

                1 1 1 1
×               1 1 0 1
———————————————————————
                1 1 1 1
              0 0 0 0
            1 1 1 1
＋         1 1 1 1
———————————————————————
        1 1 0 0 0 0 1 1
 

乘积符号为0，算后求补器输出 11000011，补[x∗y]补=011000011。
补码二进制数真值：
＋＋＋＋x∗y=0∗28＋1∗27＋1∗26＋1∗21＋1∗20=(+195)10
十进制数乘法验证：x∗y=(−15)∗(−13)=+195。

2.4 定点除法运算

2.4.1 原码除法算法原理

手算模拟除法：

上图可以发现：人工除法时，人可以比较被除数（余数）和除数的大小来确定商1(够减）或商0（不够减)。
对于机器除法，余数为正表示够减，余数为负表示不够减。不够减时必须恢复原来余数，才能继续向下运算，这种叫做恢复余数法，由于有各种判断和恢复余数的操作，控制较为复杂，不常用。

计算机常用方法：加减交替法

余数为正，商1，下次除数右移做减法;余数为负，商0，下次除数右移做加法。

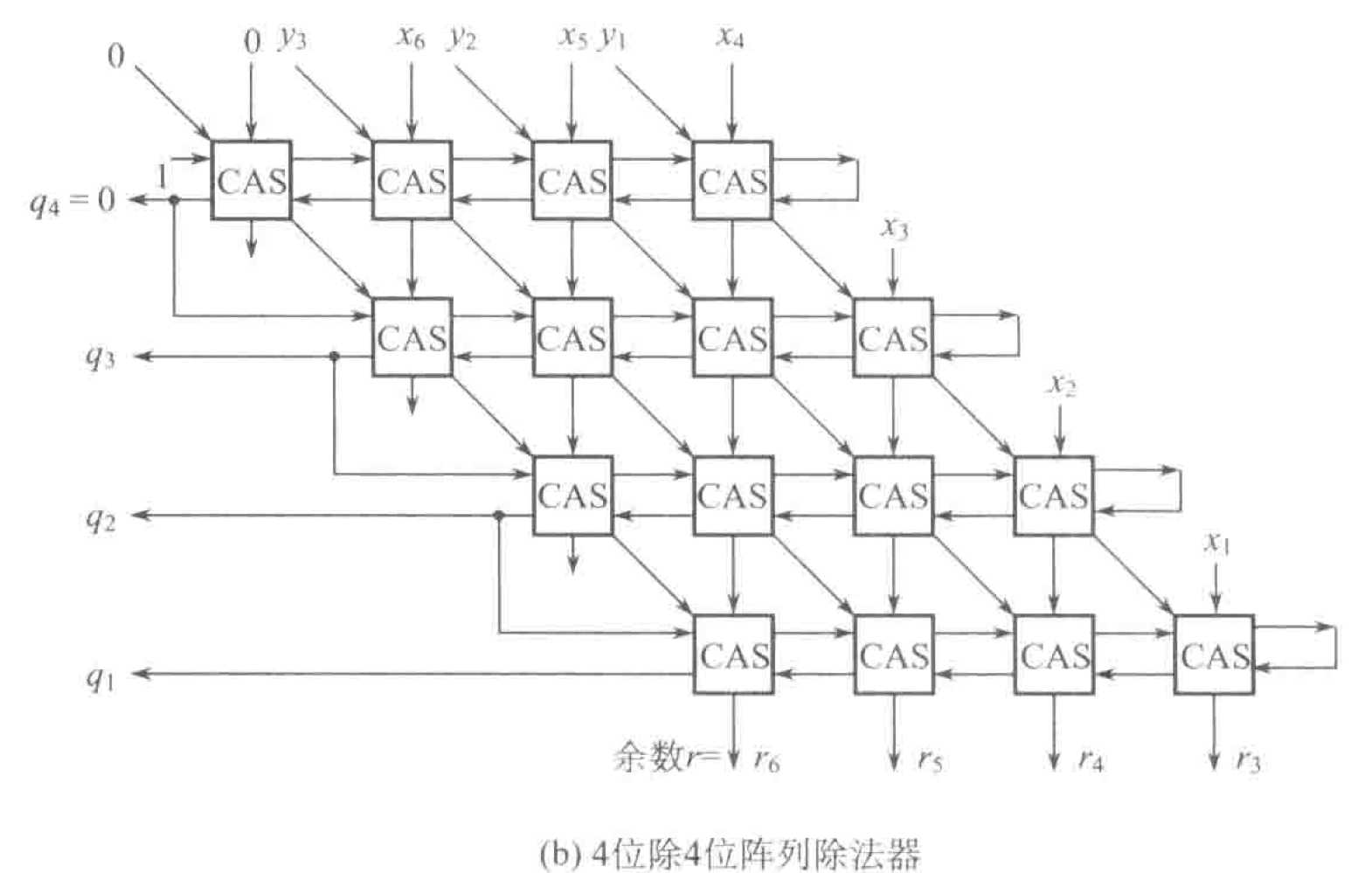
2.4.2 并行除法器

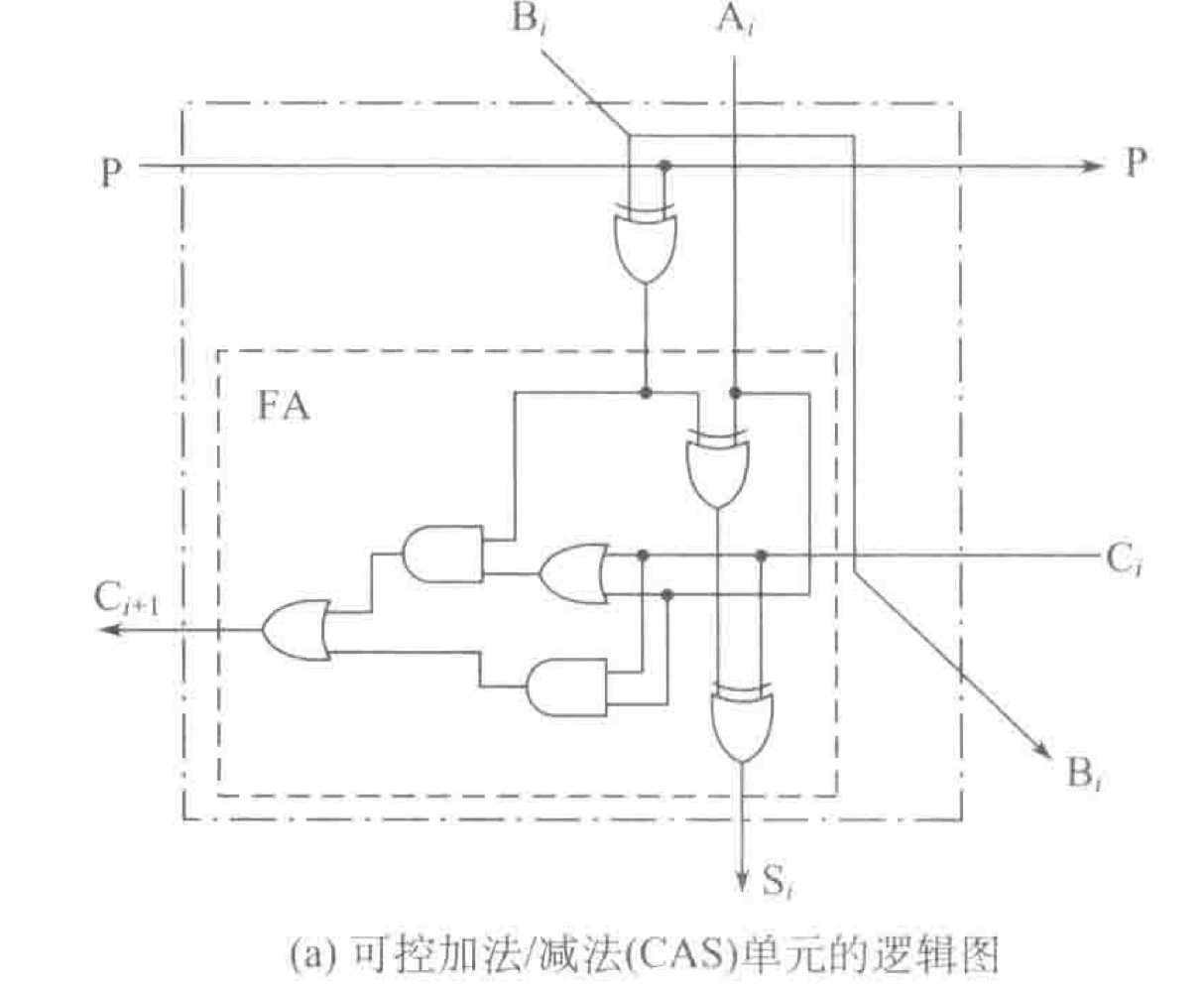
1. 可控加法减法单元（CAS）

它有四个输出和四个输入端，输入线P=0 时，CAS做加法，p=1 时，CAS做减法。
CAS的输入输出关系可以用下式表示：
Si=Ai⨁(Bi⨁P)⨁Ci
Ci+1=(Ai+Ci)⨁(Bi⨁P)+AiCi

P=1时：
Si=Ai⨁Bi⨁Ci
Ci+1=AiBi+BiCi+AiCi
P=0时：
Si=Ai⨁Bi¯⨁Ci
Ci+1=AiBi¯+Bi¯Ci+AiCi

2. 加减交替的列阵除法器

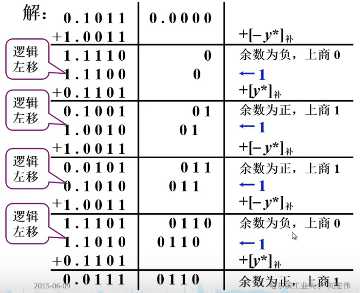
3. 例题说明

x=−0.1011 y=−0.1101, 求原[x/y]原
原原补补[x]原=1.1011[y]原=1.1101[y∗]补=0.1101[−y∗]补=1.0011

2.5 定点运算器的组成

2.5.1 逻辑运算

1. 逻辑非运算

逻辑非也称求反， 对某数进行逻辑非就是按位求反，常用变量上加一横来表示。
x=x0x1x2…xn则 x¯=x0¯x1¯x2¯…xn¯
例：x1=01001011 x1¯=10110100

2. 逻辑加运算

对两个数进行逻辑加就是按位求或，又称为逻辑或，常用“+”表示。

例：x=10100001 y=10011011 x+y=10111011

注意逻辑加是按位运算，所以没有进位！

3.逻辑乘运算

对两个数进行逻辑乘就是按位求与，又称为逻辑与，常用“·”表示。
例：x=10111001 y=11110011 x·y=10110001
注意逻辑乘是按位运算，所以没有进位！

4.逻辑异或运算

对两个数进行逻辑异或就是按位求它们的模2和，又称为按位加，常用“⨁”表示。
例：x=10101011 y=11001100 x⨁y=01100111
注意逻辑乘是按位运算，所以没有进位！

2.5.2 多功能算术/逻辑运算单元（ALU）

算术逻辑单元(简称ALU arithmetic and logic unit )

1. 同一套电路，既实现算术运算功能又实现逻辑运算功能。对数值数据的算术运算∶加、减、乘、除等对逻辑数据的逻辑运算:与、或、非运算等
2. 一种功能较强的组合逻辑电路(由与、或、非等门电路组合实现)
3. 其基本逻辑结构是超前进位加法器。

ALU不仅给出算术运算结果，还给出运算结果的特征标志。

• 例如︰算术运算是否产生了向更高位的进位，结果是否为零，结果的符号为正还是为负，结果是否溢出等。

逻辑运算通常只检查结果是否为零，不存在进位和溢出等问题。

四位ALU逻辑电路

• 分析逻辑电路：只看输入输出信号，不看电路图！

电路图

分析

• S₀~S₃

  运算选择控制决定电路执行哪种算术运算或哪种逻辑运算。

• M: 状态控制

  • 1 执行逻辑运算
  • 0 执行算术运算

• 两个参加运算的数：

  A₃A₀，B₃～B₀

  C_n : ALU最低进位

分析逻辑电路：看输入输出信号的逻辑功能表！

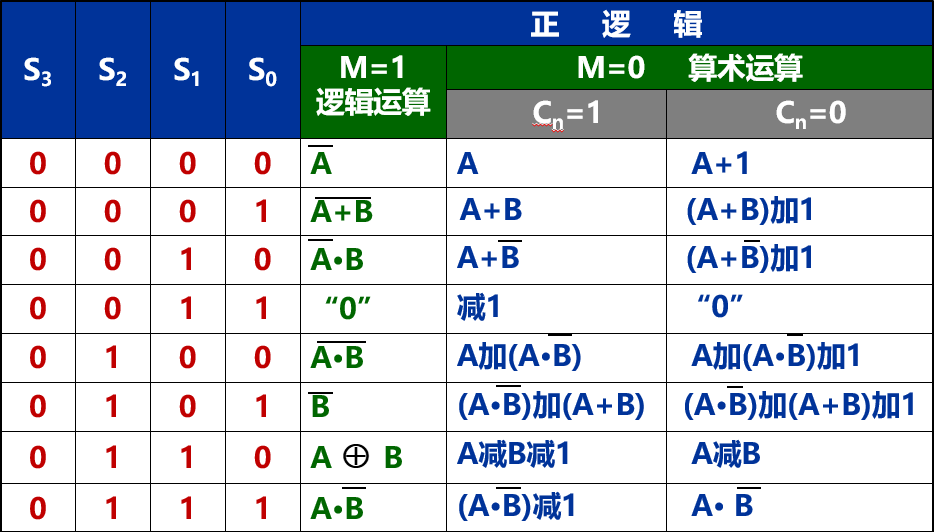
菜鸡表示什么都看不懂。。。QwQ

2.6 浮点运算方法和浮点运算器

2.6.1 IEEE754标准

**IEEE二进位浮点数算术标准（IEEE Standard for Floating-Point Arithmetic）**的标准编号,它规定了浮点数在计算机当中的存储方式以及算术标准等。

浮点格式可分为符号位s，指数位e以及尾数位f三部分。

规定了单精度（32）和双精度（64）两种基本格式（还有其他特殊格式不做介绍），规定尾数用原码，阶码用移码表示，但是不完全等同与移码，真值和阶码的转换为：单精度 E=e+127 ，双精度 E=e+1023 , E 为阶码， e 为指数真值。尾数域最高位总是1，隐藏在小数点左边不显示。

在IEEE-754 标准下，浮点数一共分为：

• NaN：即Not a Number。非数的指数位全部为1 同时尾数位不全为0。在此前提下，根据尾数位首位是否为1，NaN 还可以分为SNaN 和QNaN 两类。前者参与运算时将会发生异常。
• 无穷数：指数位全部为1 同时尾数位全为0，根据符号决定正负。
• 规格化数：指数位不全为1 同时尾不全为0。此时浮点数的隐含位有效，其值为1。
• 非规格化数：指数位全为0 且尾数位不全为0。此时隐含位有效，值为0。另外需要注意，以单精度时为例，真实指数E 并非0-127=-127，而是-126，这样一来就与规格化下最小真实指数E=1-127=-126 达成统一，形成过度。
• 0 ：指数位与尾数位都全为0，根据符号位决定正负。

IEEE754国际标准	数符	阶符+阶码(移码)	尾数(原码)	总位数
**float ** 短实数/ 单精度	1	8	23	32
double 长实数	1	11	52	64
临时实数	1	15	64	80

[阶码] =真值＋偏移量

• float偏移量=127 ,double偏移量=1023

[阶码] =真值+偏移量(浮子偏移量=127，双偏移量=1023)

[阶码]范围：0000 0001~ 1111 1110

阶码范围：-126~ +127

[尾数]=小数点前数值为1，机器存储时隐藏(尾数实际可表示24位]

2.6.2 浮点加减法

任何一个数都可以写成浮点数形式

小数点随着阶码的不同而浮动，数的范围和精度分别表示。

格式：N=S*r^j

• r : 基数, r=2 (与当前的数字的进制有关)
• j : 阶码, 带符号的纯整数(定点整数)
• S: 尾数, 带符号的纯小数(定点小数)

尾数 真值/原码 规格化, 小数点后面的数值最高为是1

比如 1100.11

我们可以化简为0.110011 * 2⁴

也可以化简为 0.0110011 * 2⁵

那么根据上面的法则, 1100.11 浮点数应该被化简为0.110011 * 2⁴

• 需要满足尾数 小数点后面的第一位是1

1.浮点加减法规则

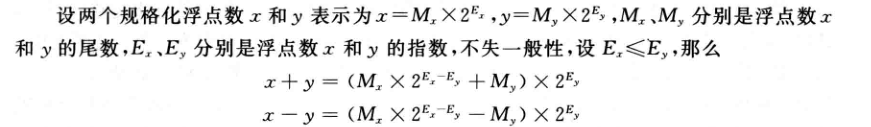
2. 运算步骤

0操作数的检查：
检查x和y中是否存在0，如果存在0则无需计算，直接得出答案。

对阶：

对阶的目的是使x 和y 的阶码相等, 使得x y 的尾数可以进行加减

将两个浮点数的阶码用补码表示，做相减运算得出需要移动的位数。遵守 小阶向大阶看齐 的原则，即小阶的尾数向右移，每移一位，阶码+1。

对阶原则

小阶向大阶看齐的原则，阶小的那个数字的尾数右移, 右移的位数等于两个数字的阶码的差值的绝对值

• 每移一位，阶码+1。

尾数加减运算：
与定点加减法运算一样，采用补码运算。

结果规格化：

上图可知：对于补码，规格化要求符号位和第一数位不同。

• 左规
  结果是00.00…001…或者11.11…110…这种形式的，没有发生溢出，不断地将尾数相对小数点向左移动一位，阶码相应-1，直到符号位和第一数位不同为止。
• 右规
  结果是01.xxxx或10.xxxx时，说明发生溢出，需要向右移动，01.xxxx向右移动一位变成00.xxxx，10.xxxx向右移动一位变成11.xxxx，阶码都相应+1。

舍入操作：

在对阶和右规过程中，可能出现尾数末尾丢失引起误差，需要考虑舍入。

• 0舍1入：类似四舍五入，丢弃的最高位为1，则进1，否则直接舍去。
• 朝0舍入：直接舍去。
• 朝+无穷舍入：正数多余位不全为“0”则进1，负数则截尾。
• 朝-无穷舍入：负数多余位不全为“0”则进1，正数则截尾。

溢出处理：

• 阶码上溢：超出阶码可能表示的最大值的正指数值，一般认为正无穷和负无穷。
• 阶码下溢：超出阶码可能表示的最小值的负指数值，一般认为0。
• 尾数上溢：尾数右移，阶码+1。
• 尾数下溢：尾数右移时最低有效位从尾数域右端流出，需要进行舍入操作。

例子：

x=0.11.1∗210 y=0.1011∗201，求 x+y （除阶符、数符外，阶码取3位，尾数取6位）

解：

补[x]补=00,010;00.110100
补[y]补=00,001;00.101100

• 对阶

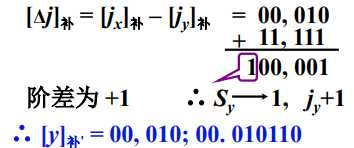
• 尾数求和

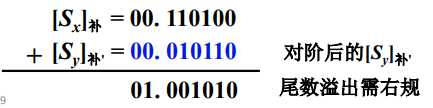
• 右规

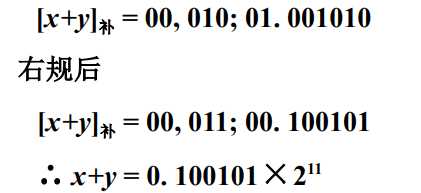
2.6.3 浮点数真值与机器数转换

已知浮点数真值x→求机器数x[浮]	真值x = ± 1.xxx…x * 2阶码
x真值:二进制	178.125 = 10110010.001
尾数规格化(小数点前是1)	1.0110010001*27
[阶码]∶阶码+偏置量127(8位)	7+127 =134 = 10000110
	134对应的8位二进制数即为阶码的移码表示
[尾数]∶隐藏小数点前的1（23位)	0110010 00100000 00000000
[x]faloat:1位符号＋8位阶码＋23位尾数	0 10000110 01100100010000000000000
已知浮点数机器数[x]浮→求真值x	机器数[x]=1位符号+8位阶码＋23位尾数
[x]float:1位符号＋8位阶码＋23位尾数	0 10000110 01100100010000000000000
x符号:	+
x阶码:8位阶码–偏置量127	10000110=134 134-127=7
x尾数:恢复小数点前隐藏的1	1.0110010001
x真值:二进制	+1.0110010001 * 27